Propondremos nuestro propio modelo de estimación de retornos a largo plazo y acto seguido intentaremos contrastar las herramientas que podemos tener a nuestro alcance para intentar estimar cada uno de los elementos del mismo, con objeto de llegar a cifras que nos ayuden en la toma de decisiones.
Punto de partida
La entrada anterior tomaba prestados unos conceptos al respecto, pues la idea de las tres componentes que ya mencionamos entonces venía de un artículo en gurufocus.com, a saber:
- Dividendos
- Crecimiento del negocio (o de la economía en su conjunto de la región* del índice que se trate)
- Cambios en la valoración/cotización
* esta componente se ve distorsionada, en cierta medida, por el carácter global de los negocios de muchas empresas, aunque estén incluidas en un índice nacional/regional concreto.
- Crecimiento del negocio (o de la economía en su conjunto de la región* del índice que se trate)
- Cambios en la valoración/cotización
* esta componente se ve distorsionada, en cierta medida, por el carácter global de los negocios de muchas empresas, aunque estén incluidas en un índice nacional/regional concreto.
Siendo el principio idéntico al de aquel artículo (descomponemos el retorno total esperado en sus componentes básicas y vemos después si se pueden estimar o predecir de alguna manera), en el presente post vamos a intentar refinar la descomposición que se hace del retorno total esperado. El objetivo es tener un modelo que no se deje fuera ninguna pieza del puzle que es nuestra inversión a largo plazo. Además, queremos que tenga cierto rigor en cuanto a clasificar la naturaleza de cada uno de los vectores que se van a identificar.
Decimos esto porque, a simple vista, ya se ve que aquel modelo que veíamos propuesto en gurufocus.com (sin querer quitarle ningún mérito), deja cosas fuera. Sin ir más lejos, excluye consideraciones fiscales respecto de los dividendos que pueden ser relevantes. Tampoco contempla qué pasa con los beneficios empresariales que no se reparten en forma de dividendos – nosotros pensamos que estos también forman parte del retorno de nuestra inversión. Lo que pasa es que aparecerán por otro lado - ahora lo veremos. Y tampoco contemplaba el impacto de los cambios en los tipos de interés (y su influencia en la tasa de descuento que debemos utilizar para estimar el valor presente de según qué flujos – lo veremos más adelante).
Como punto de partida para el modelo que vamos a explicar en nuestra entrada de hoy, también tomaremos prestados los conceptos que A Geis, D Kapp y KL Kristiansen nos detallan en su impresionante trabajo sobre cómo evoluciona la rentabilidad que se exige a la renta variable (“cost of equity”), es decir, la famosa tasa de descuento que habremos de utilizar, por ejemplo, también en nuestro modelo.
A este respecto, dichos autores definen dicha tasa de descuento como la suma del interés libre de riesgo a largo plazo más una prima (“Equity Risk Premium” o ERP) – “The cost of equity usually defines the required rate of return on equity at which future dividends are discounted and is calculated as the sum of the ERP and the long‑term risk-free rate.”
Lo veremos ahora aplicado a nuestro modelo, si bien con una considerable simplificación.
Nuestro modelo
I. Inversión directa en acciones
Si decidimos confeccionar una cartera de renta variable que no utilice vehículos de inversión colectiva (es decir, manteniendo las acciones directamente), el modelo viene a ser según se ilustra en la figura siguiente. Esta primera aproximación (inversión directa) nos va a servir para cimentar el planteamiento preferido que se explicará después, por ejemplo, con ETFs (o fondos indexados), que es el que realmente nos interesa.
Figura 1: Modelo de retorno total a un plazo largo (aunque definido) mediante inversión directa en acciones
Cuando mantenemos una cartera de acciones, nuestro retorno total a largo plazo evidentemente será igual a los dividendos netos recibidos más la variación en las cotizaciones.
Dejamos fuera, para este planteamiento:
- el impacto fiscal que tendremos a la hora de liquidar la cartera al final del periodo, pues asumimos que la mantenemos indefinidamente (tampoco contemplamos las comisiones de venta por la misma razón)
- los costes iniciales (comisiones) al adquirir las acciones, ya que no es recurrente (sólo incurrimos en ellos al principio)
- gastos de custodia, pues, si bien estos son recurrentes y habría que incluirlos si se producen, es muy fácil (¡y recomendable!) evitarlos, como ya se vio en el post anterior a este respecto
I.a. El dividendo neto recibido en el periodo a considerar
Merece la pena notar que los dividendos que percibiremos serán siempre netos de retenciones en origen y en destino.
Respecto de las retenciones en origen: El país de la empresa que distribuya los dividendos (y sus posibles acuerdos fiscales con nuestro país de residencia) determina la cuantía del porcentaje de retención (e.g. Francia 30%, Holanda 15%...). En virtud de estos potenciales acuerdos fiscales existen también mecanismos para reducir el porcentaje de dicha retención (e.g. el formulario W8 de EEUU para extranjeros, que permite bajar de un 30% a un 15%).
En cuanto a la retención en destino (en nuestro caso, España): Se nos retiene un 19% como caso general.
Para un inversor en España, existe además la posibilidad de solicitar la devolución de la menor de las dos retenciones (origen / destino) a la hora de presentar el IRPF.
(Más información sobre retenciones en origen aquí.)
I.b. La variación de las cotizaciones en dicho periodoRespecto de las retenciones en origen: El país de la empresa que distribuya los dividendos (y sus posibles acuerdos fiscales con nuestro país de residencia) determina la cuantía del porcentaje de retención (e.g. Francia 30%, Holanda 15%...). En virtud de estos potenciales acuerdos fiscales existen también mecanismos para reducir el porcentaje de dicha retención (e.g. el formulario W8 de EEUU para extranjeros, que permite bajar de un 30% a un 15%).
En cuanto a la retención en destino (en nuestro caso, España): Se nos retiene un 19% como caso general.
Para un inversor en España, existe además la posibilidad de solicitar la devolución de la menor de las dos retenciones (origen / destino) a la hora de presentar el IRPF.
(Más información sobre retenciones en origen aquí.)
La medida en que varíe la cotización de la(s) acción(es) de que se trate es precisamente la otra componente de nuestro retorno total a largo plazo.
Estimar esto a futuro no es tarea fácil, si bien parece lógico pensar que, si podemos descomponerlo en factores más sencillos, puede que resulte más fácil aproximarnos. Dichos factores los hemos identificado como:
I.b.1. Factores objetivos o racionales – esto es, sin pretender que sepamos ni que sea fácil/posible calcular su valor, lo que sí sabemos es que ese valor existe, es tangible y obedece a cierta racionalidad. Estamos hablando de:
• Los beneficios empresariales que la empresa no ha distribuido vía dividendos durante el periodo transcurrido desde que adquirimos dichas acciones hasta el final del mismo (¡o las pérdidas!, que también puede haberlas). Estas cantidades pasarán a engrosar el balance de la empresa, sea en tesorería o en cualquier otro tipo de activo/inversión a más largo plazo.
• Modificaciones que afecten a la capacidad de generación de caja en el futuro. Al final del periodo que estemos considerando, el valor de nuestra cartera habrá de recoger y reflejar dicha capacidad que se asume continúa existiendo. Hablamos del Valor Actual Neto de dichos flujos, que no es otra cosa que el valor lógico (¡racional!) que corresponde a los mismos, a saber:
I.b.2. Componentes subjetivos o irracionales de las cotizaciones – • Modificaciones que afecten a la capacidad de generación de caja en el futuro. Al final del periodo que estemos considerando, el valor de nuestra cartera habrá de recoger y reflejar dicha capacidad que se asume continúa existiendo. Hablamos del Valor Actual Neto de dichos flujos, que no es otra cosa que el valor lógico (¡racional!) que corresponde a los mismos, a saber:
Se trata, por tanto, de evaluar cómo ha variado dicha capacidad y cómo afecta dicha variación al valor de nuestra cartera al final del periodo en cuestión.
Nótese que, para empresas individuales, no parece sencillo poder tener en cuenta todos los factores internos y externos, y mucho menos la valoración de su impacto futuro. ¿Cómo variará la cuota de mercado de dicha empresa en el futuro? ¿Crecerá el sector/mercado conde opera? Más adelante veremos que esto se puede simplificar notablemente cuando hablamos de índices (a través de instrumentos de inversión colectiva).
En cualquier caso, recordemos e insistamos de cara a los siguientes apartados de nuestro post: Hablar de variación en la capacidad de generar beneficios futuros es lo mismo que hablar de variación de VALOR.
• Variación en la tasa de descuento (“i”, en nuestra fórmula del Valor Actual Neto anterior), que es determinante a la hora de objetivar el cambio en el VALOR, al final del periodo, por cuenta de las variaciones de las capacidades de generar beneficios recurrentes en el futuro por parte de las empresas de nuestra cartera. En nuestro modelo, los cambios en la tasa de descuento vendrán determinados por la variación en los tipos de interés.Nótese que, para empresas individuales, no parece sencillo poder tener en cuenta todos los factores internos y externos, y mucho menos la valoración de su impacto futuro. ¿Cómo variará la cuota de mercado de dicha empresa en el futuro? ¿Crecerá el sector/mercado conde opera? Más adelante veremos que esto se puede simplificar notablemente cuando hablamos de índices (a través de instrumentos de inversión colectiva).
En cualquier caso, recordemos e insistamos de cara a los siguientes apartados de nuestro post: Hablar de variación en la capacidad de generar beneficios futuros es lo mismo que hablar de variación de VALOR.
Recomendamos, a los efectos de comprender mejor cómo se transmiten las decisiones de política monetaria a los precios de las acciones por la vía de las tasas de descuento, leer la publicación del pasado ejercicio que ya se ha mencionado más arriba, en la web del Banco Central Europeo a este respecto: “Changes in the monetary policy stance can affect equity prices and the cost of equity via […] the interest rates employed to discount […] profits…”
Pues resulta que, en tiempos de Felipe III, el Duque de Osuna aspiraba a ser nombrado virrey de una económicamente empobrecida Nápoles, pero con considerable valor estratégico en el Mediterráneo. Fue entonces cuando su secretario, el mismísimo Quevedo, le dijo la frase que popularizó tres siglos más tarde Machado: “Sólo el necio confunde valor y precio”.
Desde #yomeloinvierto tenemos claro que lo que hemos visto en el apartado anterior como capacidad de generar beneficios futuros, cuantificada en base a una tasa de descuento, constituyen el VALOR al que se refería Quevedo. A ello añadimos, claro está (véanse las figuras), los incrementos de VALOR en libros provenientes de los beneficios no distribuidos, teniendo así la foto completa de la variación del VALOR entre dos momentos del tiempo.
Desgraciadamente, por si eso no fuera ya complicado de estimar, tenemos que aceptar que nuestro retorno total va a depender de la otra componente “necia” (por irracional), es decir, la valoración subjetiva y espuria o, mejor dicho, de su evolución entre dos momentos del tiempo. Esta adulteración del valor, si bien se muestra mucho más volátil e imprevisible en el corto plazo, tiene (¡menos mal!) una ventaja: y es que, en el largo plazo, se pone de manifiesto que no es más que un ruido, y que tiende a regresar a la senda que marca el verdadero VALOR mediante lo que llaman reversión a la media.
Aprovechamos para apuntar que existe una filosofía entera (¡y hasta una industria!) montada alrededor de la especulación con esta componente. Es nuestra opinión en #yomeloinvierto que dicha especulación con el precio a corto plazo, por mucho que se envuelva en la justificación del “análisis técnico”, prácticamente no es más que otra suerte de juego de azar. En cualquier caso, nuestra recomendación, por si se ve tentado el lector: vaya al casino y, por lo menos, ¡se lo pasará bien! (y conocerá gente, etc…)
Desde #yomeloinvierto tenemos claro que lo que hemos visto en el apartado anterior como capacidad de generar beneficios futuros, cuantificada en base a una tasa de descuento, constituyen el VALOR al que se refería Quevedo. A ello añadimos, claro está (véanse las figuras), los incrementos de VALOR en libros provenientes de los beneficios no distribuidos, teniendo así la foto completa de la variación del VALOR entre dos momentos del tiempo.
Desgraciadamente, por si eso no fuera ya complicado de estimar, tenemos que aceptar que nuestro retorno total va a depender de la otra componente “necia” (por irracional), es decir, la valoración subjetiva y espuria o, mejor dicho, de su evolución entre dos momentos del tiempo. Esta adulteración del valor, si bien se muestra mucho más volátil e imprevisible en el corto plazo, tiene (¡menos mal!) una ventaja: y es que, en el largo plazo, se pone de manifiesto que no es más que un ruido, y que tiende a regresar a la senda que marca el verdadero VALOR mediante lo que llaman reversión a la media.
Aprovechamos para apuntar que existe una filosofía entera (¡y hasta una industria!) montada alrededor de la especulación con esta componente. Es nuestra opinión en #yomeloinvierto que dicha especulación con el precio a corto plazo, por mucho que se envuelva en la justificación del “análisis técnico”, prácticamente no es más que otra suerte de juego de azar. En cualquier caso, nuestra recomendación, por si se ve tentado el lector: vaya al casino y, por lo menos, ¡se lo pasará bien! (y conocerá gente, etc…)
Siendo este el planteamiento que siempre recomendamos desde nuestro blog, resulta interesante explorar si aquí tenemos alguna ventaja a la hora de estimar los retornos a largo plazo (y ya adelantamos que sí, por la vía de la simplificación que podremos hacer del modelo anterior). Dejemos también claro desde un principio que optar por instrumentos de acumulación (en lugar de distribución, ver post anterior) va a resultar ventajoso desde el punto de vista fiscal – y no sólo para facilitar el presente análisis. Es por ello que nos centraremos en estos. A continuación, representamos el modelo.
Figura 2: Modelo de retorno total a largo plazo mediante vehículo de inversión colectiva (acumulación)
Apréciese que los factores externos que determinan los cambios en la capacidad de las empresas de nuestra cartera para generar rentas futuras quedan reducidos a un tema puramente de evolución macro (crecimiento de la economía) y, por el lado de los factores internos, de productividad (entendiendo ésta en el sentido de la optimización de los costes del negocio y la consecuencia mejora en los márgenes). Esto es así, y se aprecia claramente, si nos vamos al ejemplo extremo de una cartera multi-sectorial y global (e.g. un ETF que invierta en todo el mundo*), porque:
• deja de tener relevancia el aspecto competitivo (si una empresa pierde cuota de mercado, otra(s), también en cartera, habrá(n) de ganarla), también las modas/tendencias (si un sector pasa de moda, probablemente otro esté más en auge),
• la falta o la excelencia en la innovación, gestión, etc. que caracterice individualmente a las empresas, y que varía con el tiempo, estadísticamente se compensará entre todos los elementos constituyentes de la cartera, etc.
*Ejemplo: IE00B44Z5B48 SPDR MSCI ACWI UCITS ETF • la falta o la excelencia en la innovación, gestión, etc. que caracterice individualmente a las empresas, y que varía con el tiempo, estadísticamente se compensará entre todos los elementos constituyentes de la cartera, etc.
Merece la pena aclarar que los vehículos de inversión colectiva (ETFs, fondos), cuando reciben los dividendos de las empresas que tienen en cartera, estos también son netos de retención en origen. Otra cosa es que las jurisdicciones en donde estos están domiciliados (para nuestro caso, generalmente Irlanda o Luxemburgo), gozan de convenios que minimizan los correspondientes gravámenes efectivos en la medida de lo posible – pero pagar, pagan (más en este artículo). Lo que no tienen es el impacto de las retenciones en destino (igualmente por las jurisdicciones que eligen estos vehículos para ser domiciliados) – y de ahí las ventajas fiscales para nosotros como inversores (ver post anterior), pues al valor liquidativo/cotización del instrumento irán dichos dividendos sin retención en destino alguna.
En cualquier caso, el impacto de las retenciones en origen da lugar a un tema curioso con respecto de los índices de referencia (benchmark) que utilizan ETFs y fondos. Ya vimos en un post anterior (sobre la importancia del dividendo) que una cosa eran los índices Precio y otra los Total Return. En aquel momento no nos metimos en detalles, así que ahora añadiremos alguna consideración más, partiendo de una recapitulación breve al respecto:
• Índices Precio: Media, con la ponderación que se establezca, de la cotización (Precio) de las acciones que contenga la definición del propio índice. Esto ya lo vimos en post anteriores y es el caso sencillo.
• Índices Total Return (TR): Representan el retorno total de la cesta que se haya definido asumiendo que los dividendos brutos que reparten las empresas del índice se reinvierten inmediatamente en la proporción que establece el propio índice (sus ponderaciones). Subrayamos que se trata del importe bruto de los dividendos. Estos índices tienen cierta utilidad en EEUU, donde en muchos casos los dividendos no tributan en el caso de planes de ahorro para particulares.
• Índices netos NTR o NR: Representan lo mismo que los TR explicados arriba, sólo que asume, para su cálculo, una hipotética retención en origen de los dividendos. Por regla general son estos índices los que veremos utilizados en Europa como referencia (benchmark) de muchos de los vehículos de inversión colectiva que encontramos en el mercado.
(Ver más sobre el asunto de los tipos de índices)
Gráfico 1: Ejemplo de diferencia entre S&P 500 Total Return (línea superior) y S&P 500 Net Total Return (línea inferior). No confundir con el índice S&P 500 Precio (no mostrado).
• Índices Total Return (TR): Representan el retorno total de la cesta que se haya definido asumiendo que los dividendos brutos que reparten las empresas del índice se reinvierten inmediatamente en la proporción que establece el propio índice (sus ponderaciones). Subrayamos que se trata del importe bruto de los dividendos. Estos índices tienen cierta utilidad en EEUU, donde en muchos casos los dividendos no tributan en el caso de planes de ahorro para particulares.
• Índices netos NTR o NR: Representan lo mismo que los TR explicados arriba, sólo que asume, para su cálculo, una hipotética retención en origen de los dividendos. Por regla general son estos índices los que veremos utilizados en Europa como referencia (benchmark) de muchos de los vehículos de inversión colectiva que encontramos en el mercado.
(Ver más sobre el asunto de los tipos de índices)
Llegados a este punto estamos en condiciones de describir, de forma concisa y ordenada, a qué nos enfrentamos si queremos estimar nuestro retorno total, según este planteamiento con ETF o fondo indexado de tipo acumulación.
Método de estimación
De acuerdo con la Figura 2, correspondiente al modelo más simplificado con ETF/fondo de acumulación, pasamos a listar los elementos a estimar, así como una serie de propuestas y consideraciones al respecto de cada uno de ellos. Pero antes agrupamos los términos correspondientes al beneficio empresarial, pues nos va a ser útil más tarde para articular nuestros estimados, si bien no se pueden juntar directamente sin más, tal y como se explicará después. También ilustraremos la nomenclatura que vamos a usar en nuestra fórmula, en clara correspondencia con la misma figura anterior:
Figura 4: Modelo de retorno total a largo plazo mediante vehículo de inversión colectiva (acumulación) indicando magnitudes a calcular/estimar y agrupando términos de beneficio empresarial. “S“ denota capitalización simple; “C”, compuesta, y “T” cálculo total (ver fórmula propuesta a continuación)
De esta forma, nuestro retorno total neto (RTN%) en un periodo suficientemente largo será, en porcentaje % sobre nuestro capital invertido (lo que hemos pagado por el fondo/ETF):
RTN% tot. = Π(RDV% - ROD% - TER% + PIB%) + ∑(BND%) + MRG% tot. + ITV% tot. + RMP% tot.
Nótese que todo aquello que hace base de un ejercicio para otro (por ejemplo, los dividendos netos que percibe el fondo o ETF al ser reinvertidos por la propia gestora, o el crecimiento de la economía) no se suman para el conjunto de años en cuestión sino que se componen: (1+r)n - 1. Esto se denota en nuestra fórmula con el símbolo Π*.
Por el contrario, asumimos que los beneficios no distribuidos no hacen base, ya que, ni los reinvierte, evidentemente, el ETF, pues no han sido distribuidos, pero asumiremos que tampoco los reinvierte(n) la(s) empresa(s) (quedarían en balance), siendo este el caso más desfavorable. Por ello este retorno no lo componemos, sino que lo sumamos (∑) a modo de capitalización simple: r x n
Para las estimaciones que, si acaso, sólo se pueden construir para el periodo total y no ejercicio a ejercicio (léase las reversiones a la media o a su línea de tendencia de márgenes o valoraciones, o el impacto en el Valor Actual Neto por cambios en las tasas de descuento entre el comienzo y el final del periodo), simplemente las añadiremos como totales al final.
*Aunque estamos usando el símbolo de productorio no se trata de eso, valga la aclaración, sino de hacer la capitalización compuesta de los retornos indicados.
Incidimos de nuevo sobre el hecho de que, para una parte del beneficio empresarial (la no distribuida), asumiremos capitalización simple, mientras que para que los dividendos netos que recibe nuestro ETF y para los que, por tanto, tenemos la certeza de que son reinvertidos inmediatamente por el propio ETF, se utilizará capitalización compuesta – de ahí que, aun siendo ambas “beneficio”, haya que mantenerlas separadas.
• Como factores externos respecto de la variación del VALOR, el único relevante es el crecimiento de la economía en su conjunto (macro). Las divergencias en las políticas, las modas, tendencias, etc., que sin duda a nivel micro afectan a la empresa en su capacidad futura de generar beneficio (pues afecta directamente a la facturación), se ven compensadas entre empresas/sectores/países. Ya sólo nos interesa el conjunto de las empresas que componen el índice, por lo que sólo nos interesa la economía en su conjunto. De ahí su asimilación a la variación del PIB% en el periodo que se trate.
• Como factores internos respecto de la misma variación del VALOR, conviene también aclarar que esta componente (MRG%) pretende reflejar simplemente los ahorros de costes (y su consecuente impacto en los beneficios) derivados de la mejora secular de la productividad y que se manifiestan en la evolución de los márgenes empresariales netos medios. El impacto de los incrementos de productividad en el crecimiento (output) ya se reflejan en la componente anterior (PIB%) y debemos evitar contarlo dos veces.
• Como factores internos respecto de la misma variación del VALOR, conviene también aclarar que esta componente (MRG%) pretende reflejar simplemente los ahorros de costes (y su consecuente impacto en los beneficios) derivados de la mejora secular de la productividad y que se manifiestan en la evolución de los márgenes empresariales netos medios. El impacto de los incrementos de productividad en el crecimiento (output) ya se reflejan en la componente anterior (PIB%) y debemos evitar contarlo dos veces.
De esta forma, a esto es a lo que nos enfrentamos en nuestro estimado para el largo plazo:
Tabla 1: Propuesta para métodos de estimación según modelo
| Componente expresada en puntos % de retorno sobre nuestra inversión inicial | Propuesta de estimado | Consideraciones (ver también notas al pie de esta tabla) |
| Retorno bruto por dividendos (RDV%) y Retorno por beneficios no distribuidos (BND%) |
Se estimarán conjuntamente como Beneficio neto empresarial sobre capitalización (BNE%), y se separará posteriormente | Es necesario separar después ambas componentes porque, según se vio anteriormente, para una se asume capitalización simple y para otra, capitalización compuesta a la hora del estimado final. Ver Figura 4. |
| Para cálculo intermedio: BNE% (Beneficios netos empresariales sobre capitalización) | BNE% se calculará como el inverso de la ratio P/E* en el momento de compra | P/E ratio se define como el Precio de la acción (o la Capitalización total) dividido por el Beneficio por acción (o los Beneficios totales). De esta forma, [P/E ratio] = Capitalización / Beneficios; dividiendo numerador y denominador por la Capitalización: [P/E ratio] = 1 / [BNE%]. |
| Para estimar RDV% y BND% a partir de BNE% | La proporción entre RDV% y BND% dentro de BNE% se estimará según media histórica | A falta de históricos de pay-out ratio, se utilizarán datos históricos de dividendos. Dado que la ratio de pay-out se define como [dividendo total repartido] / [beneficio] del ejercicio, dividiendo numerador y denominador por la misma magnitud (capitalización de mercado), tenemos que (usando nuestra nomenclatura) también [Pay-out ratio] = [RDV%] / [BNE%]. |
| Retorno bruto por dividendos (RDV%) | Históricos de los últimos 5 años (mejor dato disponible) | Como proxy, podemos usar los dividendos repartidos por otros ETFs de distribución que correspondan exactamente a los mismos índices/regiones que estemos tratando – nótese que estos dividendos que reparten estos ETFs son, a su vez, los dividendos netos de retención en origen que los propios ETFs han recibido. |
| Retención en origen sobre dividendos (ROD%) | Valor típico -15% sobre dividendos | Su estimación depende también, a su vez, del estimado de la componente anterior RDV%. |
| Comisiones y gastos (TER%) | Rango típico 0,1%-0,3% (0,4% o superior en caso de fondos de RV Emergentes) | TER típico de fondos o ETFs indexados. |
| PIB% (entendido como crecimiento del VALOR por la vía del crecimiento del tamaño | Crecimiento PIB% anual estimado en el periodo que se trate | Simplificación: Ceteris paribus (mismos márgenes empresariales, etc.), un crecimiento X% de la economía resultará en idéntico crecimiento X% de los beneficios empresariales totales/absolutos y, por ende, del del VALOR actual neto de los mismos. |
| MRG% (definido como incremento de VALOR por la vía de la reducción de costes o mejora de márgenes que resulta de las mejoras en la productividad). | Reversión hacia el valor representado por la línea de tendencia secular | Se observa una tendencia histórica de los márgenes empresariales con pendiente ligeramente positiva. No obstante, en nuestro punto de partida (p.ej. el momento actual), los márgenes empresariales estarán por encima o por debajo de dicha directriz según la región del mundo (índice) de que se trate. Habrá, por tanto, que estimar la reversión hacia el valor tendencial. |
| ITV% (definido como impacto de la variación de tipos sobre el VALOR) | Modificación % del VALOR por la vía del cambio en la tasa de descuento en el momento final del periodo con respecto al inicio del mismo. ** | Se asume que dicho cambio en la tasa de descuento viene determinado por la normalización de los tipos de interés de referencia en las regiones geográficas correspondientes y se utilizará una simplificación de lo expuesto por A Geis, D Kapp y KL Kristiansen en su artículo. |
| RMP% (entendido como la eliminación a largo plazo de la infra/sobre-valoración que en un momento dado otorga el mercado) | Reversión a la media de la valoración, eliminando los efectos temporales o subjetivos sobre el precio. | Para poner dicha valoración en relación con su media histórica es necesario escoger una magnitud de referencia. Tradicionalmente se utiliza la ratio Price to Earnings (P/E), que divide la cotización por los beneficios totales (en este caso del índice/región que se trate). Warren Buffet (según nos cuenta gurufocus.com) prefiere la ratio Precio / GDP, que divide la cotización por el PIB. Esta última es la que también preferimos aquí por ser consistente con el modelo propuesto (el denominador de esta ratio es precisamente una de las componentes propuestas más arriba para la parte del VALOR). |
*Ejemplo: si asumimos que una ratio de P/E normal es 15 (mediana histórica del S&P 500), su inverso, que es 6,7%, corresponde al beneficio empresarial neto total de dicho índice S&P 500 dividido por su capitalización total de mercado (lo que hemos llamado BNE%), y se repartiría entre la rentabilidad bruta por dividendos (RDV%) más el beneficio no distribuido (BND%).
** El delta de Valor actual neto en % (nuestro ITV%) como función de delta de la tasa de descuento “i” resulta sencillo de aproximar si lo asimilamos al NPV de una renta perpetua: NPV = C / i, luego la variación en % de NPV de un escenario inicial (1) a un escenario final (2) resulta = i1/i2 -1.
Apoyándonos en lo expuesto en el trabajo ya mencionado (web del ECB), la tasa de descuento i sería la suma del interés libre de riesgo a largo plazo más una prima de riesgo (“Equity Risk Premium” o ERP), que a su vez sería el retorno exigido sobre el capital (renta variable) y que coincide con el inverso de la ratio P/E (price to earnings). Nosotros vamos a asumir que la parte que es prima de riesgo (ERP) permanece constante y que un cambio en el tipo de interés libre de riesgo a largo plazo (que a su vez se mueve paralelamente a la variación del tipo de referencia del banco central) se va a traducir íntegramente en un cambio de idéntica magnitud en la tasa de descuento i.
“[…] the ratio of stock prices to the […] earnings. When inverted, it gives the average earnings to current prices, also known as the historical earnings yield […] it is also clear that the inverse […] ratio measures the absolute return on equity and not the excess return over the risk‑free rate”
Por tanto, i1 sería la tasa de descuento que resulta de hacer el inverso de la ratio P/E en el momento de compra, e i2 sería el nuevo valor tras sumarle a i1 el delta de tipos de interés de referencia correspondiente a una normalización de los mismos.
(Se recomienda revisar nuestro Glosario de Términos para aclarar conceptos).
Insistimos de nuevo (ya se vio en la última figura) en que, para las magnitudes [RDV% - ROD% - TER% + PIB%], se aplicará capitalización compuesta en el periodo del que pretendamos estimar el retorno de nuestro fondo/ETF de acumulación. Para BND% se aplicará capitalización simple en el mismo periodo. Y para el resto (MRG%, RMP% y ITV%) se contemplará un único impacto porcentual total en cada caso a sumar/restar para calcular el retorno total, según la variación en sus factores determinantes desde el momento actual hasta el final del periodo para el que se pretenda prever dicho retorno.** El delta de Valor actual neto en % (nuestro ITV%) como función de delta de la tasa de descuento “i” resulta sencillo de aproximar si lo asimilamos al NPV de una renta perpetua: NPV = C / i, luego la variación en % de NPV de un escenario inicial (1) a un escenario final (2) resulta = i1/i2 -1.
Apoyándonos en lo expuesto en el trabajo ya mencionado (web del ECB), la tasa de descuento i sería la suma del interés libre de riesgo a largo plazo más una prima de riesgo (“Equity Risk Premium” o ERP), que a su vez sería el retorno exigido sobre el capital (renta variable) y que coincide con el inverso de la ratio P/E (price to earnings). Nosotros vamos a asumir que la parte que es prima de riesgo (ERP) permanece constante y que un cambio en el tipo de interés libre de riesgo a largo plazo (que a su vez se mueve paralelamente a la variación del tipo de referencia del banco central) se va a traducir íntegramente en un cambio de idéntica magnitud en la tasa de descuento i.
“[…] the ratio of stock prices to the […] earnings. When inverted, it gives the average earnings to current prices, also known as the historical earnings yield […] it is also clear that the inverse […] ratio measures the absolute return on equity and not the excess return over the risk‑free rate”
Por tanto, i1 sería la tasa de descuento que resulta de hacer el inverso de la ratio P/E en el momento de compra, e i2 sería el nuevo valor tras sumarle a i1 el delta de tipos de interés de referencia correspondiente a una normalización de los mismos.
(Se recomienda revisar nuestro Glosario de Términos para aclarar conceptos).
Aplicación del modelo
Poco sentido tendría llegar hasta aquí con nuestro modelo si luego no nos tomamos la molestia de intentar aplicarlo. Para ello vamos a hacer dos ejemplos. Intentaremos estimar a un plazo de 10 años* lo que sería el retorno total esperado para un producto (ETF/fondo) indexado a un índice de renta variable emergente y también para uno indexado a un índice de renta variable de los países desarrollados. Ahí va:
*Dado que el modelo incluye componentes cuya estimación es simplemente la reversión a uno valores / tendencias medias, al elegir un plazo estamos implícitamente asumiendo que, al final del mismo, el cumplimiento de dichas reversiones tiene lugar en su totalidad. Evidentemente esto no tiene por qué cumplirse justo para el plazo que arbitrariamente hemos puesto, pero sí que se cumplirá en algún momento. Por tanto, utilícese el modelo con más cautela aún, si cabe. Análogamente, se asume también que en el instante final del periodo escogido nos encontramos una situación de tipos de interés normalizados; ello, si bien puede o no cumplirse en ese instante, sería esperable que se produjera en algún momento del tiempo. Lo dicho: cautela.
Tabla 2: Ejemplos de estimación de retorno total utilizando como plazo un periodo de 10 años y para 2 instrumentos de inversión colectiva de acumulación.
| Componente (ver notas explicativas sobre el cálculo de cada dato bajo la tabla) | Desarrollados Ejemplo: IE00BFY0GT14 SPDR MSCI World UCITS ETF |
Emergentes Ejemplo: IE00BKM4GZ66 iShares Core MSCI Emerging Markets IMI UCITS ETF |
| BNE% como inverso de la ratio P/E inicial en el momento de compra (nota 1) | = 1 / 17.26 = 5,79% (se divide en los valores a continuación) |
= 1 / 12,61 = 7.93% (se divide en los valores a continuación) |
| RDV% bruta como rentabilidad por dividendo neta según históricos (nota 2) dividida por (1 - 15%) | = 2,59% / 0.85 = 3,05% (anual en capitalización compuesta) |
= 2,82% / 0.85 = 3,31% (anual en capitalización compuesta) |
| BND% como diferencia BNE% - RDV% anteriores | = 5,68% - 3,05% = 2,63% (anual en capitalización simple) |
= 8.59% - 3,31% = 5,28% (anual en capitalización simple) |
| ROD% como -15% de la rentabilidad por dividendo bruta estimada anteriormente | = -0.15 x 3,05% = -0,45% (anual en capitalización compuesta) |
= -0.15% x 3,31% = -0,50% (anual en capitalización compuesta) |
| TER% de cada ETF (nota 3) | -0,12% (anual en capitalización compuesta) |
-0,18% (anual en capitalización compuesta) |
| PIB%, siendo este el crecimiento futuro anual según estimados disponibles (nota 4) | 1,5% (anual en capitalización compuesta) |
4,4% (anual en capitalización compuesta) |
| MRG%; se descarta el estimado disponible para los cambios en el VALOR por la vía de los márgenes netos (nota 5) | Se asume margen neto de las empresas (y, por tanto, del VALOR por esta vía) sin cambios al final del periodo | Se asume margen neto de las empresas (y, por tanto, del VALOR por esta vía) sin cambios al final del periodo |
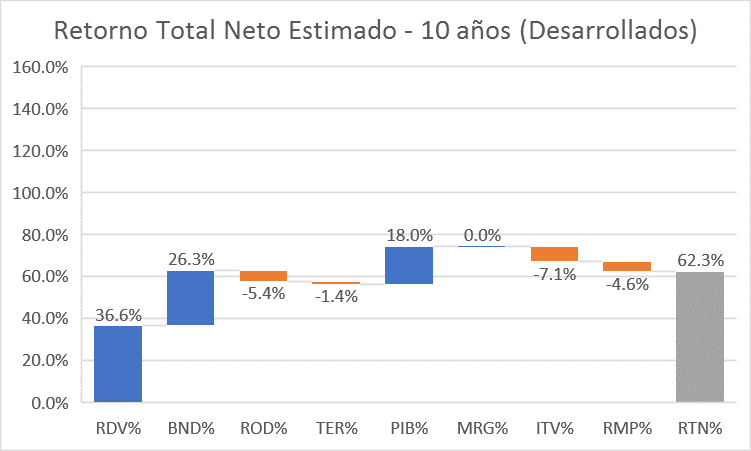
| ITV% como impacto en el VALOR por la vía de la normalización de los tipos de interés, según fórmula del NPV (nota 6) | i1/i2 - 1 = [5,79% / (5,79% + 0,44%)] -1 = -7,1% (total periodo) |
i1/i2 - 1 = [7.93% / (7.93% + 1,75%)] -1 = -18,1% (total periodo) |
| RMP% como impacto esperado en precio se la ratio considerada (Capitalización/PIB) regresa a su media (nota 7) | -4,6% (media ponderada a partir de datos de gurufocus.com) (total periodo) |
5,3% (media ponderada a partir de datos de gurufocus.com) (total periodo) |
| RTN% (Retorno Total Neto estimado para vehículo indexado, tipo acumulación, a 10 años, según modelo, a partir de los estimados de sus componentes anteriores) * | RTN% = (1+3,05%-0,45%-0,12%+1,5%)^10 - 1 + (2,63% x 10) -7,1% -4,6% = 62,3% (total)
Equivale, para el periodo de 10 años establecido, a una TIR de 5,0% |
RTN% = (1+3,31%-0,50%-0,18%+4,4%)^10 – 1 + (5,28) x 10) - 18,1% +5,3% = 137,3% (total)
Equivale, para el periodo de 10 años establecido, a una TIR de 9,0% |
Sección con las notas correspondientes a los de datos incluidos en la Tabla 2 anterior (si algún lector se la salta, prometemos no tenérselo en cuenta):
Nota 1
Nota 2
Nota 3
Nota 4
Nota 5
Nota 1
En el momento de escribir este post, según documentos de MSCI (Desarrollados y Emergentes).
Nota 2
Estimados de rentabilidad neta por dividendo – tomamos el "5Y yield on Cost" (que viene a ser la media anual del retorno por dividendo durante los últimos 5 años referida al coste inicial de compra) de ETFs de distribución equivalentes: (Desarrollados, iShares MSCI World ETF, y Emergentes, iShares Core MSCI Emerging Markets ETF).
Nota 3
Según justetf.com, para los ETFs elegidos en nuestros ejemplos de la tabla (Desarrollados, IE00BFY0GT14 SPDR MSCI World UCITS ETF, y Emergentes: IE00BKM4GZ66 iShares Core MSCI Emerging Markets IMI UCITS ETF).
Nota 4
Informe de HSBC septiembre 2018.
“Growth in both emerging and developing markets between now and 2030 will slow. Emerging economies are projected to grow by 4.4 per cent a year compared to 4.7 per cent in the period since 2010, while developed countries will grow by 1.5 per cent, compared with 1.7 per cent since 2010.”
“Growth in both emerging and developing markets between now and 2030 will slow. Emerging economies are projected to grow by 4.4 per cent a year compared to 4.7 per cent in the period since 2010, while developed countries will grow by 1.5 per cent, compared with 1.7 per cent since 2010.”
Nota 5
1. Constatamos que ambas regiones presentan valores y tendencias de fondo similares en lo que se refiere a márgenes empresariales netos (Fuente, Bloomberg).
2. Recurrimos a yardeni.com (informe) para extraer una tendencia histórica, en este caso, del S&P 500 (es de lo que hay más datos – como solución de compromiso asumiremos que esta tendencia es válida para ambos ejemplos de nuestro modelo, en virtud de lo dicho en el punto 1 anterior):
Ello resulta en una línea de tendencia con una pendiente aproximada de 1 punto de margen neto adicional por década, con el último valor disponible sin desviación aparente considerable respecto de dicha tendencia.
Si contáramos 1 punto extra de margen neto de las empresas (sobre el 8% actual) de aquí al final del plazo de los 10 años propuesto para los ejemplos, ello supondría un incremento de VALOR del 12% (ver razonamientos sobre el modelo en apartados anteriores).
Por parecernos exagerado, este dato se desestima y asumiremos, para ambos ejemplos, que los márgenes empresariales no varían en el periodo (retorno por esta componente 0%). Esto tendrá la ventaja, al menos, de situar nuestro estimado final del lado más conservador.
Nota 62. Recurrimos a yardeni.com (informe) para extraer una tendencia histórica, en este caso, del S&P 500 (es de lo que hay más datos – como solución de compromiso asumiremos que esta tendencia es válida para ambos ejemplos de nuestro modelo, en virtud de lo dicho en el punto 1 anterior):
Ello resulta en una línea de tendencia con una pendiente aproximada de 1 punto de margen neto adicional por década, con el último valor disponible sin desviación aparente considerable respecto de dicha tendencia.
Si contáramos 1 punto extra de margen neto de las empresas (sobre el 8% actual) de aquí al final del plazo de los 10 años propuesto para los ejemplos, ello supondría un incremento de VALOR del 12% (ver razonamientos sobre el modelo en apartados anteriores).
Por parecernos exagerado, este dato se desestima y asumiremos, para ambos ejemplos, que los márgenes empresariales no varían en el periodo (retorno por esta componente 0%). Esto tendrá la ventaja, al menos, de situar nuestro estimado final del lado más conservador.
Para el cálculo estimativo se procede según el siguiente esquema:
a. Desarrollados:
Nota 7
1. Compararemos los tipos actuales (de los bancos centrales) en los países de nuestros respectivos índices con el consenso existente para su normalización.
2. Las diferencias halladas se aplicarán sobre la actual tasa de descuento. Para este ejercicio consideramos, de acuerdo con lo ya explicado en la exposición del modelo, la tasa resultante de calcular el inverso de la ratio de P/E en el momento de compra.
3. A continuación, aplicaremos la fórmula vista en la Tabla 1 anterior (i1/i2 - 1) para calcular el impacto en puntos porcentuales sobre su VALOR presente.
2. Las diferencias halladas se aplicarán sobre la actual tasa de descuento. Para este ejercicio consideramos, de acuerdo con lo ya explicado en la exposición del modelo, la tasa resultante de calcular el inverso de la ratio de P/E en el momento de compra.
3. A continuación, aplicaremos la fórmula vista en la Tabla 1 anterior (i1/i2 - 1) para calcular el impacto en puntos porcentuales sobre su VALOR presente.
a. Desarrollados:
a.1. Si tomamos como normalización la vuelta a los niveles de 2000 – 2007 (anteriores a la crisis), tenemos a EEUU justo en su valor, a la Eurozona 2,7 puntos por debajo y a Reino Unido 2,35% también por debajo. Asumimos que Japón no se va a mover.
Ponderando según composición del índice (11% para Eurozona y 6% para Reino Unido – no hace falta incluir los que ya están en su nivel neutro, como EEUU y Japón; y obviamos los más pequeños), tenemos:
b. Emergentes:Ponderando según composición del índice (11% para Eurozona y 6% para Reino Unido – no hace falta incluir los que ya están en su nivel neutro, como EEUU y Japón; y obviamos los más pequeños), tenemos:
2,7% x 0,11 + 2,35% x 0,06 = 0,44%
a.2. La tasa de retorno base (actual) corresponde al inverso de la ratio de P/E:
i1 = 1/17,26 = 5,79%
a.3. Calcularemos el impacto total en el valor:
ITV% = i1/i2 - 1 = [5,79% / (5,79% + 0,44%)] -1 = -7,1%
b.1. Análogamente (datos de ceicdata.com), nos encontramos con que China estaría 2,5 puntos por debajo de su nivel “normalizado”, Corea 3 puntos, Taiwán 1 punto, Brasil 6 puntos e India en su nivel.
Ponderando según composición del índice (29% China, 14% Corea, 12% Taiwán, 9% India y 8% Brasil – obviamos el resto):
Ponderando según composición del índice (29% China, 14% Corea, 12% Taiwán, 9% India y 8% Brasil – obviamos el resto):
2,5% x 0,29 + 3% x 0,14 x 1% x 0,12 + 6% x 0,08 = 1,75%
b.2. La tasa de retorno base (actual) como inverso de la ratio de P/E:
i1 = 1 / 12,61 = 7.93%
b.3. Impacto en el total valor:
ITV% = i1/i2 - 1 = [7.93% / (7.93% + 1,75%)] -1 = -18,1%
El impacto en precio por la vía de la reversión a la media de la ratio Capitalización / PIB lo ha calculado gurufocus.com (recomendamos leer el informe completo, si bien consideramos que su modelo carece de algunos de los elementos que sí hemos incluido en el nuestro) y es el dato que vamos a utilizar (si bien tenemos que trabajarlo un poco):
1. Sabemos que nuestro índice de países Desarrollados “MSCI World” lleva un 62% de EEUU, un 9% de Japón y un 3% de Alemania (el resto lo obviamos por tener poco valor en la gráfica o poco peso en el índice). Una aproximación mediante media ponderada sería, a partir del gráfico: -7% x 0,62 - 1% x 0,09 - 4% x 0,03 = -4,6%
2. Por otro lado, nuestro índice de Emergentes “Core MSCI Emerging Markets” lleva un 29% de China, un 9% de India y un 4% de Rusia (asumimos que el resto de componentes o bien ya está en su media o no son significativos por tamaño). Análogamente: RMP% emergentes = 16% x 0,29 + 2% x 0,09 + 13% x 0,04 = 5,3%
2. Por otro lado, nuestro índice de Emergentes “Core MSCI Emerging Markets” lleva un 29% de China, un 9% de India y un 4% de Rusia (asumimos que el resto de componentes o bien ya está en su media o no son significativos por tamaño). Análogamente: RMP% emergentes = 16% x 0,29 + 2% x 0,09 + 13% x 0,04 = 5,3%
Conclusión
En primer lugar, se constata que, si bien el modelo parece más sólido que lo que teníamos como punto de partida, no por ello hemos de tomar los estimados que arroja como algo seguro y 100% fiable.
Como el lector habrá podido apreciar en la sección correspondiente a las notas sobre los detalles de los estimados, ha habido que realizar numerosas asunciones y simplificaciones debido a la falta de datos. Por otro lado, es también cierto que esto no es otra cosa que una cuestión de medios. Las imprecisiones derivadas de dichas asunciones o simplificaciones no serían, por tanto, en principio, achacables al modelo.
Lo que sí es achacable al modelo es el hecho de que descansa sobre unas asunciones que se han incluido en su propia definición, y que no podemos olvidar ya que pueden perfectamente no cumplirse, a saber: Justo al final del periodo que se elija, se está asumiendo que hay una serie de magnitudes que se “normalizan” con respecto a sus valores del principio del mismo:
- Asumimos que los márgenes empresariales vuelven a su valor de tendencia secular (si bien esto no hemos podido aplicarlo en los ejemplos)
- Se da por hecho, también, que las infra/sobre- valoraciones desaparecen por la vía de la reversión a la media de la ratio que se trate (en este caso Capitalización / PIB).
- Se toma como cierta una normalización de tipos de interés a los efectos de su impacto en la tasa de descuento para estimar las variaciones del VALOR.
- Se da por hecho, también, que las infra/sobre- valoraciones desaparecen por la vía de la reversión a la media de la ratio que se trate (en este caso Capitalización / PIB).
- Se toma como cierta una normalización de tipos de interés a los efectos de su impacto en la tasa de descuento para estimar las variaciones del VALOR.
Un par de consideraciones adicionales que son relevantes antes de pasar a las palabras finales:
¿Qué pasa con la inflación?
Con la divisa pueden surgir dos cuestiones. En primer lugar, respecto a cubrir o no la divisa a la hora de tener una cartera de renta variable (sin ir más lejos, los ETFs de los ejemplos). Recomendamos revisar la entrada anterior de este blog al respecto (si bien, por resumir, diremos que se recomienda no cubrir la divisa y, de hecho, los ETFs de los ejemplos no las cubren).
La segunda cuestión que podemos plantear se refiere a si el retorno que se ha estimado tiene o no en cuenta las posibles fluctuaciones de las divisas de los países con respecto a nuestra divisa base. Análogamente a lo visto respecto de la inflación, dependerá de qué input introduzcamos en el modelo, concretamente (de nuevo) en la parte que corresponde al crecimiento del PIB. Dicha tasa de crecimiento suele estar (por ejemplo, si tomamos el Banco Mundial) ya referida a una misma moneda (a efectos prácticos el dólar), luego contempla aquellos efectos que pudieran derivarse de las divergencias entre las divisas que sea (por ejemplo, de los distintos países emergentes) y la divisa de referencia. Por decirlo de otra forma: el consenso a futuro del 4,5% de crecimiento anual de los países emergentes ya es en dólares constantes, y es lo que, en nuestro caso, estamos introduciendo en el modelo.
Finalmente -
El modelo nos va a dar el retorno real (después de inflación) o nominal (teniendo que descontar la inflación después) dependiendo de qué magnitudes usemos como input del mismo.
En nuestro caso, al haber tomado estimados de crecimiento real del PIB (que no nominal), es decir, ya ajustado por inflación, ya estamos determinando que el cálculo final sea también real, es decir, que es un retorno que representa lo que “nos sobra” después de cubrir la inflación que se dé en cada ejercicio.
¿Y con la divisa?En nuestro caso, al haber tomado estimados de crecimiento real del PIB (que no nominal), es decir, ya ajustado por inflación, ya estamos determinando que el cálculo final sea también real, es decir, que es un retorno que representa lo que “nos sobra” después de cubrir la inflación que se dé en cada ejercicio.
Con la divisa pueden surgir dos cuestiones. En primer lugar, respecto a cubrir o no la divisa a la hora de tener una cartera de renta variable (sin ir más lejos, los ETFs de los ejemplos). Recomendamos revisar la entrada anterior de este blog al respecto (si bien, por resumir, diremos que se recomienda no cubrir la divisa y, de hecho, los ETFs de los ejemplos no las cubren).
La segunda cuestión que podemos plantear se refiere a si el retorno que se ha estimado tiene o no en cuenta las posibles fluctuaciones de las divisas de los países con respecto a nuestra divisa base. Análogamente a lo visto respecto de la inflación, dependerá de qué input introduzcamos en el modelo, concretamente (de nuevo) en la parte que corresponde al crecimiento del PIB. Dicha tasa de crecimiento suele estar (por ejemplo, si tomamos el Banco Mundial) ya referida a una misma moneda (a efectos prácticos el dólar), luego contempla aquellos efectos que pudieran derivarse de las divergencias entre las divisas que sea (por ejemplo, de los distintos países emergentes) y la divisa de referencia. Por decirlo de otra forma: el consenso a futuro del 4,5% de crecimiento anual de los países emergentes ya es en dólares constantes, y es lo que, en nuestro caso, estamos introduciendo en el modelo.
Respecto a los valores estimados de retorno neto que hemos encontrado al final, una cifra anual (TIR a partir del retorno total neto estimado a 10 años) del 5% para nuestro ETF de mercados desarrollados y un 9% para el de emergentes, hemos de decir que son algo más bajos que los que estima gurufocus.com. Dicha diferencia, sin embargo, se explica, sobre todo (aunque hay, por supuesto, más cosas), por los estimados de crecimiento del PIB que se han utilizado en ambos casos – las fuentes no son, evidentemente, las mismas y la nuestra es, claramente, más conservadora (ver nota 4 arriba).
En cualquier caso, algo que probablemente ya sabíamos, puesto que se ha dicho en entradas anteriores del blog (y las magnitudes de fondo tampoco han cambiado tanto): la renta variable emergente está, en estos momentos, más barata que la de las zonas desarrolladas y, por tanto, es de esperar un retorno mayor a largo plazo (en nuestro caso, una diferencia de 4 puntos porcentuales por ejercicio).
Ahí queda, pues, nuestro modelo para estimar retornos a largo plazo – no es perfecto, pero siempre será mejor que mirar la bola de cristal.En cualquier caso, algo que probablemente ya sabíamos, puesto que se ha dicho en entradas anteriores del blog (y las magnitudes de fondo tampoco han cambiado tanto): la renta variable emergente está, en estos momentos, más barata que la de las zonas desarrolladas y, por tanto, es de esperar un retorno mayor a largo plazo (en nuestro caso, una diferencia de 4 puntos porcentuales por ejercicio).
La Bola de Cristal














No me cansaré de repetir que es el blog de bolsa con más calidad que he encontrado. Artículo muy denso y que tendré que releer varias veces. Muchas gracias, sigue así.
ResponderEliminar